프로그래머스 코딩테스트 연습을 하면서 dfs(깊이 우선 탐색)에 관하여 공부할 기회가 있어 적어보고자 한다.
프로그래머스 코딩테스트 연습>완전탐색>소수찾기
문제설명
자리 숫자가 적힌 종이 조각이 흩어져있습니다. 흩어진 종이 조각을 붙여 소수를 몇 개 만들 수 있는지 알아내려 합니다.
각 종이 조각에 적힌 숫자가 적힌 문자열 numbers가 주어졌을 때, 종이 조각으로 만들 수 있는 소수가 몇 개인지 return 하도록 solution 함수를 완성해주세요.
제한사항
- numbers는 길이 1 이상 7 이하인 문자열입니다.
- numbers는 0~9까지 숫자만으로 이루어져 있습니다.
- "013"은 0, 1, 3 숫자가 적힌 종이 조각이 흩어져있다는 의미입니다.
입출력 예
| numbers | return |
| "17" | 3 |
| "011" | 2 |
출처 : 프로그래머스 코딩테스트
dfs(깊이 우선 탐색 - 나무위키)는 트리 또는 그래프를 탐색을 하는 과정에서 최대한 깊게 탐색을 한 후 다른 루트로 탐색을 진행하는 방식이다. 모든 경우의 수를 전부 고려하기 위한 경우에 주로 사용한다. 이외로는 bfs와 최선 우선 탐색 따위가 있다. 코딩 공부를 하면서 이번에 처음 알게된 개념이어서 기록 해두고 작성한 코드를 기록해 두고자 한다.
dfs방식은 깊이를 우선 탐색하기 때문에 최우선으로 구조의 마지막까지 도달하게 되고 마지막을 확인 한 후 원하는 결과가 아니 경우 그 과정에서 확인해 둔 갈림길로 돌아가서 다시 마지막까지 탐색하는 것을 반복하는 방식이다.
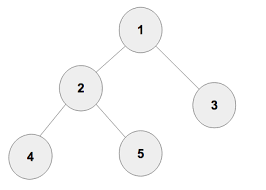
dfs 탐색순서 :
1번 노드에서 출발 -> 2번 확인 -> 4번 확인 -> (2번으로 돌아와서) 5번 확인 -> (1번으로 돌아와서) 3번 확인
위와 같은 순서로 탐색을 진행하여 전체를 확인 할 수 있는 방법이다. 장점은 원하는 결과가 깊이 있을 경우 탐색이 용이하다. 현 경로상의 노드만을 기억하면 되므로 메모리가 적게 필요하다. (예: 우측 이미지의 5번을 탐색할 때 필요한 노드는 1,2,5이다.) 단점은 무한 루프등에 취약하다. 깊이가 무한이 있을 경우에는 한계점을 설정할 필요가 있다. dfs를 이용하여 얻는 결과가 최단 경로인 것은 아니다라는 점도 있다.
위키에서 제안한 것과 같이 각 노드가 가지는 경로를 기억하는 변수, 각 노드의 방문 여부를 기록하는 변수와 재귀함수를 이용하여 구현했다.
상단의 문제를 풀기위해서 답안으로 제출했던 코드이다. 아래에서 visit()함수가 dfs를 구현한 함수이고 index_nodes, index_visited가 각각 노드별 경로와 방문여부를 dict형식으로 저장해둔 변수이다. 문제에서 필요한 것은 모든 인덱스를 1번씩 거치는 것이 아니라, numbers를 구성하는 문자열로 만들어 질수 있는 모든 조합이 필요하기 때문에 1번 방문을 했더라도 재방문이 필요했다. 따라서, 마지막 노드를 방문 후 갈림길로 되돌아오는 과정에서 방문여부(True, False)를 변경하면서 진행하게 하여 전체 조합의 만들어 냈다.
def solution(numbers):
answer = 0
nums = list(numbers)
check_num = []
def prime(num:int):
max_ran = int(num ** 0.5 + 1)
for i in range(2,max_ran):
if num % i == 0:
return False
return True
index_nodes = {str(i):[str(j) for j in range(len(numbers)) if j != i] for i, a in enumerate(numbers)} # 인덱스를 노드로 설정
index_visited = {i:False for i in index_nodes.keys()} # 인덱스 방문 여부 확인
def visit(n, temp): # dfs 함수, 수 찾기
if index_visited[n]: return
temp += n
check_num.append(temp)
index_visited[n] = True
for i in index_nodes[n]:
visit(i, temp)
index_visited[n] = False
for i in index_nodes.keys():
temp = i
check_num.append(temp)
index_visited[i] = True
for j in index_nodes[i]:
visit(j, temp)
index_visited[i] = False
check_num = list(set(int("".join([numbers[int(n)]for n in num])) for num in check_num)) # 수찾기 완성
for i in range(2):
if i in check_num:
check_num.remove(i)
answer = sum(list(map(prime, check_num)))
return answer
정수로 변환하기 전의 결과물(check_num)을 보자면 첫 번째 예제에서는 ['0', '01', '1', '10'], 두 번째 예제에서는 ['0', '01', '012', '02', '021', '1', '10', '102', '12', '120', '2', '20', '201', '21', '210']와 같이 나열된다. 아쉬운 부분은 index번호를 이용하여 모든 조합을 찾아냈기 때문에 2번째 예시에서 겹치는 부분(1과 1, 11(index: 12)과 11(index: 21))과 같이 동일한 숫자를 제외하지 못했다는 점이 다소 아쉽다.
사실 이번에 공부를 하면서 손으로 직접 해당 문제를 푸는 것은 대단히 어렵지 않으나, 이를 컴퓨터 언어로 표현하고 작동하게 하기 위해서 굉장히 막막했다. 단순히 for문을 7개(문제의 제한사항)를 사용하거나, while을 이용하여 반복하여 구하거나 하는 등 고민을 했지만 비효율적이고, 적확하다고는 할 수 없어 고민하고 공부하는 과정에서 dfs를 알게 되었다. 이후에는 bfs 및 다른 검색 방법 등 확인해보고자 한다.
아. 다른 사람의 풀이를 봤을 때, 조합을 구하는 함수 itertools.permutations(iterable, r)을 이용하여 보다 직관적이고 간편하게 푼 답안이 있었다... 그래도 새로운 알고리즘에 대해 공부한 기회와 재귀함수를 이용한 알고리즘 구현에 성공하여 좋은 기회라고 생각한다. 재귀함수는 사용은 할 수 있으나, 직관성이 부족하다고 느껴지기 때문일까 기능 또는 개념을 직접 설계하는데 사용하는데는 아직 어려움이 있다.
'개발자 공부 > 코딩테스트' 카테고리의 다른 글
| 버블정렬 - 시간복잡도 O(N^2)으로 비효율적이지만 쉬운 정렬 (0) | 2025.03.23 |
|---|---|
| DataStructure Heap / Programmers 코딩테스트 - 이중우선순위큐 (0) | 2024.07.09 |
| 알고리즘 - 프로그래머스 입문 구슬을 나누는 경우의 수: 자료형으로 인한 문제 (0) | 2024.05.20 |
| 상수 실습 feat.programmers (0) | 2023.10.20 |
